Game of Life 1: Display
Game of Life display
In this part of the assignment, we’ll implement enough code to display a world state as part of our implementation of Conway’s Game of Life in Racket.
There will be a fair bit of set up in the next section, where you’ll need to copy this code into your Racket file, but you won’t have to write anything new. After we can make some simple configurations and random worlds, however, then you’ll get to write some code to implement the drawing of a world.
![]() Look for the Racket icon, which
we’ll use to mark exercises you need to complete.
Look for the Racket icon, which
we’ll use to mark exercises you need to complete.
The world state and examples
As discussed on the overview page, our big-bang
world state will be a list of
the “live” cells in the world, where each cell is just going to be
a posn holding the the x- and y-coordinates of that cell on the
grid. So a world is a list of posns, where each posn contains two numbers:
; live-cell: posn
; world: [posn]
As some examples that will be useful in testing, here are world states that represent the block, blinker, and glider configurations.
(define block
(list (make-posn 0 0)
(make-posn 0 1)
(make-posn 1 0)
(make-posn 1 1)))
(define blinker
(list (make-posn 0 0)
(make-posn 0 1)
(make-posn 0 2)))
(define glider
(list (make-posn 1 0)
(make-posn 2 1)
(make-posn 0 2)
(make-posn 1 2)
(make-posn 2 2)))
These correspond to  ,
,  , and
, and  respectively.
respectively.
You’ll want to copy these into your code since they’ll be useful for testing as we move forward.
Building a random state and testing unknown orders
To “see things happen” it’s useful to be able to create a random world. Rather than have you do that, I’m just going to provide you with code for that. Again, you’ll want to copy this into your Racket file so you can use it to display random world states.
We’ll start with a function make-all-cells that creats all the
posns in the given range. This is a fairly complex use of apply,
build-list and multiple lambdas, so definitely ask questions if
you’re not clear what’s happening here.
; make-all-cells makes a list of all the (x, y)
; pairs where x and y are in the range [0, x-max - 1]
; and [0, y-max - 1) respectively.
; make-all-cells: number, number -> [posn]
(define (make-all-cells x-max y-max)
(apply append
(build-list
x-max
(lambda (x)
(build-list
y-max
(lambda (y) (make-posn x y)))))))
To test make-all-cells is a little tricky, because we don’t want
the test to be tied to a particular ordering of the cells returned
by make-all-cells. The definition above returns the cells in
some particular order, but there’s nothing special about that ordering,
and any other ordering would also be correct. This will be true for many
functions as we move forward, so it’ll useful to solve this problem now.
A standard approach is to sort the lists that we get so we know what order they’re in. If, for example, we have a team of three people, Sally, Chris, and Pat, and we ask for a list of their names, we could get any of a number of orders for their names. If we sort the list we get, though, then there should be exactly one result:
(list "Chris" "Pat" "Sally")
So here we’ll take the list we get back from make-all-cells and sort
it using a function posn< (copy this one as well). We’ll also sort
our list of the expected posns, and have check-expect compare those
lists. If they have the same set of posns, then sorting should ensure
that the lists match exactly and the check-expect should succeed.
; posn< returns #true if p comes before q in lexicographical
; (essentially alphabetic) order, i.e., if the x-coordinate
; of p is smaller than the x-coordinate for q, or they have
; the same x-coordinates and the y-coordinate of p is less
; than the y-coordinate of q.
(define (posn< p q)
(or (< (posn-x p) (posn-x q))
(and (= (posn-x p) (posn-x q))
(< (posn-y p) (posn-y q)))))
(check-expect
(sort (make-all-cells 3 3) posn<)
(sort (list (make-posn 0 0)
(make-posn 0 1)
(make-posn 0 2)
(make-posn 1 0)
(make-posn 1 1)
(make-posn 1 2)
(make-posn 2 0)
(make-posn 2 1)
(make-posn 2 2)) posn<))
Now that we have make-all-cells, we can remove half of
those cells at random to generate a random board:
; random-world creates a list of random
; cells with x- and y-coordinates in the range
; [0, x-max - 1] and [0, y-max - 1] respectively.
; Each cell in that space has a 50% chance of being
; included in the resulting list.
; random-world: number, number -> [posn]
(define (random-board x-max y-max)
(filter (lambda (c) (zero? (random 2)))
(make-all-cells x-max y-max)))
Testing a function like random-world is also tricky
because the result is, by definition, random and thus
not predictable. So what we’ll do here is confirm that
all the x- and y-coordinates are in the correct range:
(check-satisfied
(random-world 10 5)
(lambda (posns)
(andmap (lambda (p) (and (<= 0 (posn-x p))
(< (posn-x p) 10)
(<= 0 (posn-y p))
(< (posn-y p) 5)))
posns)))
Drawing a world
Now that we can make some simple configurations like a block, and a
random world, we need to be able to draw it. Remember that big-bang
will pass our rendering function a world state, which is going to be
a list of the posns of the “live” cells.
First, let’s define some useful constants:
; The radius, in pixels, of a circle representing
; a "live" cell.
(define cell-radius 2)
; A little white space between cells.
(define padding 1)
; The diameter of a cell in pixels, plus a pixel
; padding. Each cell's square will be cell-size by cell-size.
(define cell-size (+ padding (* 2 cell-radius)))
; The size of the rendered version of the board,
; measured in cells, not pixels.
(define board-x 100)
(define board-y 100)
; The number of blank pixels to place on each side (top, bottom,
; left, and right) around the world. This prevents the display
; of cells from running up against the edge of the scene.
(define board-padding 20)
Exercise 1: place-cell
![]() Write a function
Write a function place-cell that places a cell on a given background
image. This should take into account the board-padding and the
cell-size in deciding on the placement of the circle representing
that cell.
Some examples:
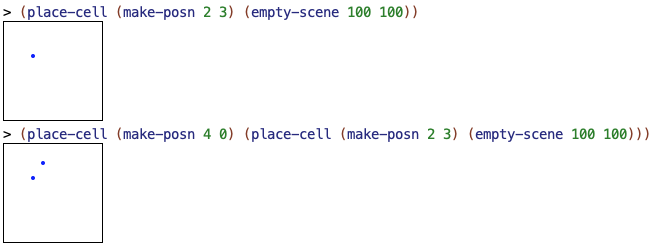
check-expect tests that correspond to these two calls:
(check-expect
(place-cell (make-posn 2 3) (empty-scene 100 100))
(place-image
(circle 2 "solid" "blue")
30 35
(empty-scene 100 100)))
(check-expect
(place-cell (make-posn 4 0)
(place-cell (make-posn 2 3) (empty-scene 100 100)))
(place-image
(circle 2 "solid" "blue")
40 20
(place-image
(circle 2 "solid" "blue")
30 35
(empty-scene 100 100))))
You should copy these into your Racket file to give you a start on your testing.
⚠️ Note!!! These tests are full of “magic” numbers
like 2, 30, 35, etc. These are the correct values, but your code
should not be full of magic numbers like this. You should instead
use named constants like cell-radius and padding to build the
relevant numbers. If you have questions about this definitely ask
ASAP.
⚠️ I’m using the color "blue" for my circles, so you’ll need to
use "blue" as well to get these tests to pass. One could argue
that I should have added another named constant for that color
instead of scattering the “magic string” "blue" all over the
code. Alternatively I could have written a draw-cell function
that encapsulates both "solid" and "blue" so they’re only
in one place. I’ll save that for another day.
To understand the math behind the numbers in the tests, it might help to look at a diagram:

Here the center of cell (0, 0) will be
(world-padding, world-padding)
since that’s how far we need to shift that first cell over and down. In the write-up the value of world-padding is 20, so that means the center of this cell will be (20, 20).
For other cells, we want to shift over/down by multiples of cell-size based on the posn-x and posn-y of the cell. The x-coordinate of the center of the cell at (2, 3), for example, will be:
world-padding + 2 * cell-size
Using the values given in the write-up this will be
20 + 2 * 5 = 20 + 10 = 30
Similarly the y-coordinate will be
world-padding + 3 * cell-size = 20 + 3 * 5 = 20 + 15 = 35
This is where the 30 and 35 come from in the first check-expect
for place-cell.
Make sure you use the named constants (e.g., world-padding)
and not the “raw” numbers (e.g., 20) when implementing
place-cell. You want to be able to change the value of things
like world-padding and have the whole drawing system update
accordingly.
Exercise 2:draw-world
![]() Write a function
Write a function draw-world that takes a world state (i.e., a
list of posns representing the live cells in that state) and
draws that world.
A simple example:

This just shows the top of the scene since the rest is empty and not terribly informative.
A check-expect test corresponding to this example is:
(check-expect
(draw-world (list (make-posn 2 3) (make-posn 4 0)))
(place-image
(circle 2 "solid" "blue")
40 20
(place-image
(circle 2 "solid" "blue")
30 35
(empty-scene 540 540))))
⚠️ Note!!! Again, this is full of magic numbers that shouldn’t
appear in your code. As example, where do the 540 values come from
that define the size of the background scene? Here world-x and
world-y are both 100, so we should have room for 100 cells in both
dimenions. How big is a cell? cell-size which, if you do the math
in its definition above, is 5 in this case. That means we need
500 by 500 pixels for the cells. If we then add 20 pixes of padding
(from world-padding) twice for each dimension (left and right for
the horizontal, and top and bottom for the vertical), we end up
with 540 for both dimensions. That math should be captured in your
code so that if we change, e.g., cell-radius, all the drawing
would update accordingly.
This is the first function that acts on a list. You can implement
this using recursion on lists, or you can use something like foldr
to combine the list of posns into a single value, which is an image
in this case.
You can also use this to draw some of the provided patterns, e.g., you can draw a glider:

You should also be able to draw the block and the blinker, and any other patterns you wish to add to your Racket file. The Wikipedia entry has numerous other examples to play with if you’d like.
You can also draw random worlds:

Note that if you call (draw-world (random-world 100 100)) you’ll get
a different pattern than the one above because random-world
generates a different, random world every time we call it.
Originally written by @elenam, with subsequent modifications by @NicMcPhee