Game of Life 2: Neighbors
Background
In this part of the assignment, we’ll implement the idea of the neighborhood of a cell, and counting the number of neighbors that a cell has. as part of our implementation of Conway’s Game of Life in Racket. This is an important step in our eventual determination of whether a cell is alive or dead in the next generation.
There will definitely be more functions to implement here than in the previous part, so start early and ask lots of questions.
I’ve provided a few tests for some of the problems, but you will probably want/need to write additional tests to handle cases that the given tests don’t cover, and to make sure you understand what a function is supposed to do.
Also, be sure to provide a description and signature for any functions you write in this exercise. You can probably extract the basic information for the description from the problem statement. If you’re not sure what the signature should be for a given function, definitely ask.
Shifting a cell/posn
A useful tool for this and several other parts of the
implementation is the idea of shifting a cell or
posn, using another posn to specify how much the
x- and y-coordinates should be shifted.
Consider this test:
(check-expect
(shift-cell
(make-posn 3 7)
(make-posn 2 -4))
(make-posn 5 3))
Here we want to shift the cell/posn (3, 7) to the right
by 2 and up by 4 (represented by (make-posn 2 -4)).
The result would then be 5 (i.e., 3 + 2) for the new
x-coordinate and 3 (i.e., 7 + -4) for the
new y-coodinate.
Exercise 1:shift-cell
![]() Write a function
Write a function shift-cell that takes two posns
and returns a new posn that is the result of shifting
the first by the amounts specified in the second. You
should certainly pass the test given above, but you want to also include some additional tests.
Exercise 2: shift-cell-list
![]() Write a function
Write a function shift-cell-list that takes a list
of cells and a single posn representing the amounts to
shift by, and apply that shift to every cell in the
list.
This should pass, for example, these tests:
(check-expect
(shift-cell-list
(list (make-posn 5 8)
(make-posn 9 6)
(make-posn 3 2))
(make-posn -2 6))
(list (make-posn 3 14)
(make-posn 7 12)
(make-posn 1 8)))
(check-expect
(shift-cell-list blinker (make-posn 3 7))
(list (make-posn 3 7)
(make-posn 3 8)
(make-posn 3 9)))
where blinker is as defined in
the previous set of exercises.
Make sure to provide additional tests; what, for
example, shift-cell-list return if the input list
is empty?
Generating neighbors
The key action when running the Game of Life is to determine how many live cells are neighbors of a given cell. A natural way to do this “on paper” is to go to each cell and count the number of live cells around it. The problem there is that we have a potentially infinite set of cells we could/should do this counting for, and computers aren’t good at doing something for an infinite collection of cells in a reasonable amount of time.
As an example, consider this example:

As a human, we wouldn’t bother counting the live neighbors of the cell with the question mark, because it’s “obvious” to us that there are no live cells near it and it’s neighbor count would be zero. Computers are pretty terrible at “obvious”, though, and if we count the neighbors for every cell, we’ll probably end up counting the neighbors for that cell as well. Worse, we’ll count the neighbors for many cells (possibly infinitely many) that are nowhere close to any live cells, which is terribly inefficient. In the example above, only 8 cells have a live neighbor, with 16 cells (twice as many) having no live neighbors.
This suggests an alternative approach, however. Instead of going to every cell and count its neighbors, go to every live cell and make a list of it’s neighbors. We can then combine all these lists, and see which cells appear in that list 2 or 3 times. If a cell is in the list twice, and it’s already alive, it stays alive. If it’s in the list three times, it’s alive in the next generation regardless of whether it was alive or not in this generation. Since we’re modeling the world as just a list of the live cells, we don’t need to do anything with any cell that didn’t appear in the list (like our question mark cell above), appeared only once, or appears more than 4 times.
Consider this example
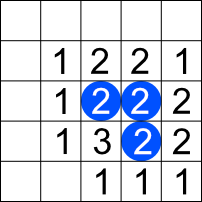
The numbers are the number of occurrences of each cell that is the neighbor of one of the three live cells. Note that we haven’t had to do anything for the empty cells; they weren’t adjacent to a live cell so they never got generated in a list of neighbors.
Given this list of cells and counts, we can
- Ignore all the cells with counts 1.
- Make any cell with a count of 3 live, regardless of whether it’s currently alive or not.
- Keep any live cells with a count of 2 alive.
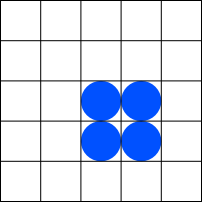
That would then lead to the following state:
Exercise 3: generate-neighbors
![]() Write a function
Write a function generate-neighbors that takes a
cell/posn and returns a list of cells/posns that are
the neighbors of the given cell.
This should, for example, pass the following tests:
(check-expect
(sort (generate-neighbors (make-posn 7 3)) posn<)
(sort (list (make-posn 6 2)
(make-posn 6 3)
(make-posn 6 4)
(make-posn 7 2)
(make-posn 7 4)
(make-posn 8 2)
(make-posn 8 3)
(make-posn 8 4)) posn<))
(check-expect
(sort (generate-neighbors (make-posn 0 0)) posn<)
(sort (list (make-posn 1 1)
(make-posn 1 0)
(make-posn 1 -1)
(make-posn -1 1)
(make-posn -1 0)
(make-posn -1 -1)
(make-posn 0 1)
(make-posn 0 -1)) posn<))
(Note the use of sort here so that the tests will pass
if you return the correct posns regardless of their
order.)
There are many reasonable ways you can do this.
One is to generate a list of eight posns representing
the eight offsets from a given cell, and then use
the shift-cell-list function you just wrote to apply
all those to the given cell. You can do that with map
in a nice way, or you can use explicit recursion if
you prefer.
Exercise 4: all-neighbors
![]() Write a function
Write a function all-neighbors that takes a world
state (a list of cells/posns) and retuns a new list
of cells/posns that is all the neighbors of every
cell in the given world state. Note that some cells
may appear multiple times in the list; this is
desirable and important.
Below is a test for a world state containing two cells
with a blank cell between them. Note that there are
several duplicates, namely (4, 6), (4, 7), and
(4, 8), each of which is a neighbor of both the
cells in the given world state.
(check-expect
(sort
(all-neighbors
(list (make-posn 3 7)
(make-posn 5 7))) posn<)
(sort
(list
; Neighbors of (make-posn 3 7)
(make-posn 2 6)
(make-posn 2 7)
(make-posn 2 8)
(make-posn 3 6)
(make-posn 3 8)
(make-posn 4 6)
(make-posn 4 7)
(make-posn 4 8)
; Neighbors of (make-posn 5 7)
(make-posn 4 6)
(make-posn 4 7)
(make-posn 4 8)
(make-posn 5 6)
(make-posn 5 8)
(make-posn 6 6)
(make-posn 6 7)
(make-posn 6 8)) posn<))
And here’s a test where the given world state is a horizontal blinker:
(check-expect
(sort
(all-neighbors
(list
(make-posn 7 2)
(make-posn 8 2)
(make-posn 9 2))) posn<)
(sort (append
(generate-neighbors (make-posn 7 2))
(generate-neighbors (make-posn 8 2))
(generate-neighbors (make-posn 9 2)))
posn<))
There’s a nice solution to this using map and
apply append. Or you could do it with one of the fold
functions. Or you could use explicit recursion. So many
options!
Originally written by @elenam, with subsequent modifications by @NicMcPhee